浙教版数学七年级上知识点总结(1)

文档可直接打印使用,更多完整内容请关注官方网址https://jiandanjie.com 查询 或关注 #小程序:说明书指南

#公众号: 说明书指南

以下仅提取部分文档的文字供展示

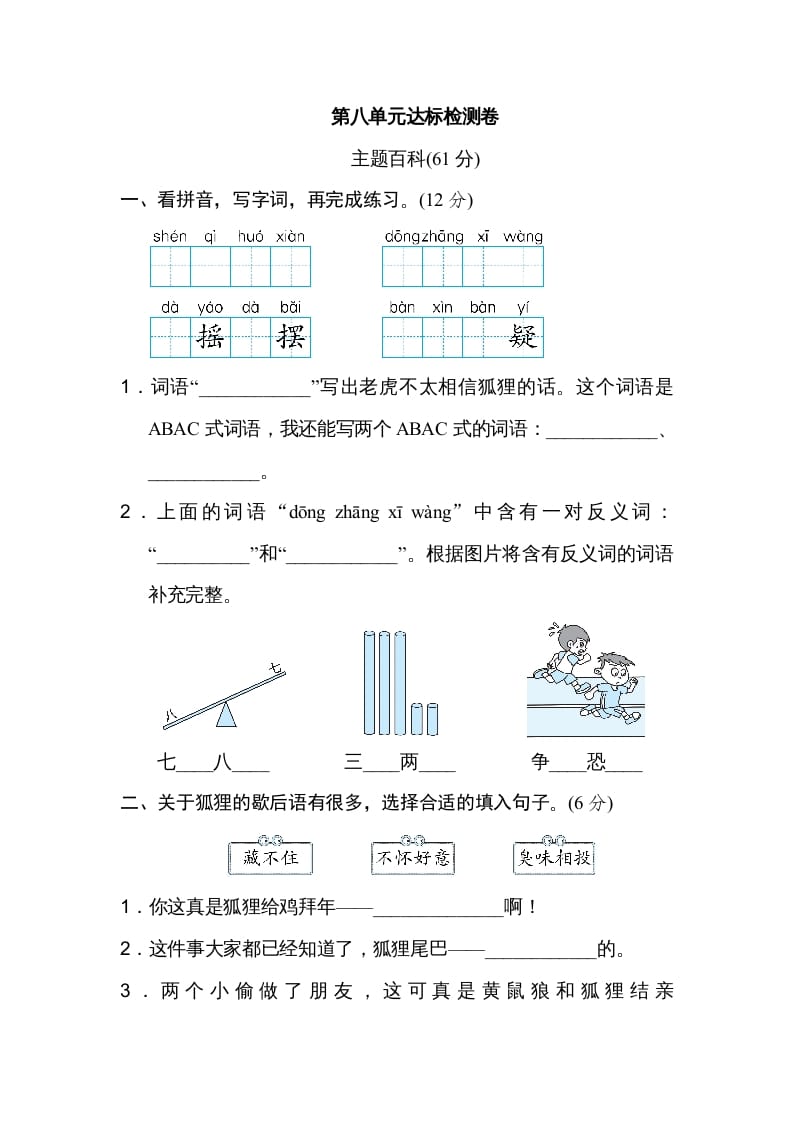
浙教版数学七年级上册知识点汇总
第一章 有理数及其运算

正整数(如:1 2，3……)
整数| 零(0)
负整数(如:1 2 3

1 1
正分数(如 到邓 5 38

分末多要几:-上-上 -23 48.

1 整数，包含正整数和负整数，分数包含正分数和负分数。正整数和正分数通称为正数，负整数和负分数通称为负
数。正整数和负整数通称为自然数
2. 正数，都比 0 大，负数比 0 小，0 既不是正数也不是负数。
正整数、0、负整数、正分数、负分数这样的数称为有理数.
数轴的三要素! 原点、正方向、单位长度〔三者缺一不可)。
任何一个有理数，都可以用数轴上的一个点来表示。(反过来，不能说数轴上所有的点都表示有理数)
3. 相反数， 只有符号不同的两个数互为相反数，4和-a 互为相反数，0 的相反数是 0。
在任意的数前面添上“-”号，就表示原来的数的相反数。
在数轴上，表示互为相反数的两个点，位于原点的侧，且到原点的距离相等。
数轴上两点表示的数，右边的总比左边的大。正数在原点的右边，负数在原点的左边。
和绝对值: 数轴上一个数所对应的点与原点的距离叫做该数的绝对值，用“| | ”表示。
正数的绝对值是它本身，负数的绝对值是它的相反数，0 的绝对值是0。

aa>0) | 二 -大
或 lal

lalj oe=0 ””，，， ，
汪 村本本
有 ala<0) 21012 3 即，当4是正数时， + 当0是负数时，l|= -a:， 当a=0时， 5.绝对值的人性质，除 0 外，绝对值为一正数的数有两个，它们互为相反数， 互为相反数的两数《除0 外) 的绝对值相 任何数的绝对值总是非负数，即jal>0

@@对任何有理数a，都有1al>0
加阁| 则1al=0，反之亦然
轿若lal=b，则a=tb

轩对任何有理数a都有|al=|-al

6 .比较两个负琢的大小，绝对值大的反而小。比较两个负数的大小的步骤如下:

@@先求出两个数负数的绝对值，

轩比较两个绝对值的大小

国根据“两个负数，绝对值大的反而小“做出正确的判断。
了7. 两个负数比较大小，绝对值大的反而小-
8. 数轴上的两个点表示的数，右边的总比左边的大-

第二章” 有理数的运算

工 有理数加法法则:。 同号两个数相加，取相同的符号，并把绝对值相加。
号的两个数相加，绝对值不等时，取绝对值较大的数的符号，并用较大的绝对值减去较小
ndanjie.com-学科网简单学习一条街 https://jiandanjie.com

的绝对值。互为相反数的两数相加得 0.
一个数同 0 相加仍得这个数
2灵活运用运算律，使用运和简化，通常有下列规律;
国互为相反的两个数，可以先相加，
@@符号相同的数，可以先相加;
国分母相同的数，可以先相加;
@几个数相加能得到整数，可以先相加。
3. 加法交换律: a+六= +

条加法结合律: (a+D)+c= a+(p+c)

5 .有理数减法法则。减去一个数等于加上这个数的相反数。
6.有理孝胰法法则，两数相季，同号得正，异号得负，绝对值相乘。储何数与0相乘积仍得 0。
7了.有理数减法运算时注意两”变”，人改变运算符号;
@@改变减妆的性质符号〈变为相反数)
a 有列数减法运算时注意一个”不变”，被减数与茂数的位置不能变换，也就是说，减法没有交换律。
有理数的加减法混合运第的步归，@ 写成省略加号的代数和。在一个算式中，若有碱法，应由有理数的减法法则
转化为加法，然后再省略加号和括号:
@@利用加法则，加法交换律、结合律简化计算。
《注意。减去一个数等于加上这个数的相反数，当有减法统一成加法时，数应变成它本身的相反数。)

9.俩数，如果两个数互为全数，则它们的乘积为 1。(如: 2 、 了
10 .有理数各法法则。 G)症数相乘，同号得正，异号得负，绝对值相生

加任何数与0 相乘，积仍为0。
11. 乘法交换律:ab = ba

12. 乘法结合律: (ab)c = Ga(bc)

13. 乘法分配律， (w+人xc= ac+bc

乘法的交换律、结合律、分配律在有理数运算中同样适用。
144.有理数乘法运算步骤，()先确定积的符号;
@@求出各因数的绝对值的积。
乘积为 1 的两个有理数互为倒数。注意:
@@零没有倒数
@@求分数的倒数,就是把分数的分子分及凑合位置.一个带分数要先化成假分数。
国正数的倒数是正数，负数的倒数是负数。
15. 有理数除法法则;, 除以一个不等于 0 的数，等于委这个数的倒数。
* 两个有理数相除，同号得正，异号得负，绝对值相除。0除以任何数都得 0，且 0不能作除
数，否则无意义。
16.有再数的乖方，求n 个相同因数4 的积的运算叫做乘方，乘方的结果叫做守。

名
we
axaxax-xa=[ 0二
守
在@中@叫做底数，n 叫做指数，@读作@ 的na 次守 (或@的次方)。

注意: @一个数可以看作是本身的一次方，如 5=51;
四当底数是负数或分数时，要先用括号将底数括上，再在右上角写指数。

17 .乘方的运算性质:
国正数的任何次蛙都是正数;
2
简单人 ndanjie.com-学科网简单学习一条街 https://jiandanjie.com

@@和负数的奇次罕是负数，负数的偶次罕是正数;
辐任何数的偶数次罕都是非负数，
图1 的任何次坚都得1，0 的任何次守都得 0;
加-1 的偶次蛙得 1; -1 的奇次坚得-1;
加在运算过程中，首先要确定宕的符号，然后再计算宕的绝对值。
18.有理数混合运算法则:， (GD)先算乘方,再算乘除,最后算加减。
加如果有括号,先算括号里面的。
19. 渴合运算顺序: 。 先算乘方，再乘除，后加减:
。 同级运算，从左到右进行:
。 如有括号，先算括号内的运算，按小括号、中括号、大括号依次进行。
20 .近似数和有效数字:
与实际相符的数，叫做准确数
与实际接近的数，叫近似数
21. 有效数字: 一般地，一个近似数四含五入到哪一位，就说这个近似数精确到哪一位这时，从左边第一个非零数
字起到精确到那一位数字止，所有的数字

第三章 。 实数

王一般地如果一个数的平方根等于 a,那么这个数叫做a 的平方根.也叫 3 的二次方要.
一个正数有正负两个平方根,它们互为相反数丸 的平方根是 9;负数没有平方根.
正数的平方根称为算数平方根.
2 .实数定义: 有理数与无理数统称为实数。
3。实数的分类: 无理数，无限不循环小数叫无理数。
有理数: 整数和分数统称有理数。

无理数定义:
即非有理数之实数，不能写作两整数之比。若将它写成小数形式，小数点之后的数字有无限多个，并且不会循环。
常见的无理数有大部分的平方根、x 和 e〈其中后两者同时为超越数) 等。

无理数是无限不循环小数。如圆周率 x 、 反 等。

无理数性质:

无限不循环的小数就是无理数 。换名 就是不可以化为整数或者整数比的数
性质 1 无理数加《减) 无理数既可以是无理数又可以是有理数

性质 2 无理数乘〈除) 无理数既可以是无理数又可以是有理数

性质 3 无理数加《减)》有理数一定是无理数

性质 4 无理数乘(除) 一个非0 有理数一定是无理数

无理数与有理数的区别:

1、把有理数和无理数都写成小数形式时，有理数能写成有限小数和无限循环小数，
是 要

比如;14 0，和-0.8，30. 333

而无理数只能写成无限不循环小数，
比如，代= 4213562-
根据这一点，人们把无理数定义为无限不循环小数;

ndanjie.com -学科网简单学习一条街 https://jiandanjie.com