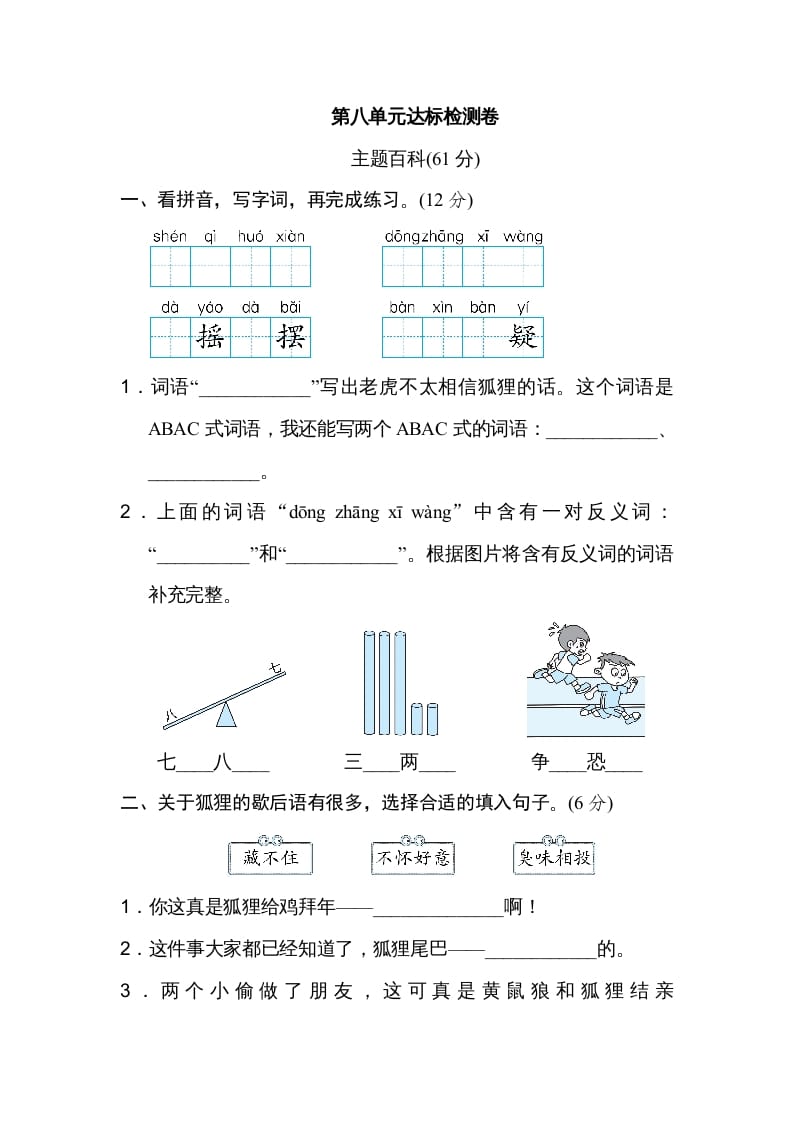
六年级数学下册2、逆向分析思路

文档可直接打印使用,更多完整内容请关注官方网址https://jiandanjie.com 查询 或关注 #小程序:说明书指南

#公众号: 说明书指南

以下仅提取部分文档的文字供展示

【逆向分析思路】从题目的问题入手，根据数量关系，找出解这个问题所需

要的两个条件，然后把其中的一个(或两个) 未知的条件作为要解决的问题，再
找出解这一个 (或两个) 问题所需的条件; 这样逐步逆推， 直到所找的条件在题
里都是已知的为止，这就是逆向分析思路，运用这种思路解题的方法叫分析法。

例 1 两只船分别从上游的A 地和下游的 B 地同时相向而行，水的流速
为每分钟 30 米,两船在静水中的速度都是每分钟 600 米， 有一天，两船又分别
从A、8 两地同时相向而行，但这次水流速度为平时的 2 倍，所以两船相遇的地
点比平时相遇点相差 60 米，求A、B 两地间的距离。

分析〈用分析思路考虑) :

(1) 要求A、B8 两地间的上距离，根据题意需要什么条件?

需要知道两船的速度和与两船相遇的时间。

(2) 要求两船的速度和，必要什么条件?

两船分别的速度各是多少。题中已告之在静水中两船都是每分钟 600
米，那么不论其水圳是否改变，其速度和均为 (600+600) 米，这是因为顺水
船速为: 船速+水速，逆水船速为; 船速-水速，故顺水船速与逆水船速的和为:
船速+水速+船速-水速=2 个船速〈实为船在静水中的速度)

(3) 要求相遇的时间，根据题意要什么条件?

两次相遇的时间因为距离相同，速度和相同，所以应该是相等的，这就
是说，尽管水流的速度第二次比第一次每分钟增加了 30 米，仍不会改变相遇时
间, 只是改变了相遇地点: 偏离原相遇点 60 米, 由此可知两船相遇的时间为 60

=30=2 (小时) 。

此分析思路可以用下图

例 2 五环图由内径为 4，外径为 5 的五个圆环组成, 其中两两相交的小
曲边四边形 (阴影部分) 的面积都相等 (如图 2.4) ，已知五个圆环六住的总面
积是 122.5，求每个小曲边四边形的面积 (圆周率r取 3.14)

图2.4 亲

分析 (〈仍用逆向分析思路探索) :

(1) 要求每个小曲边四边形的面积，根据题意必须知道什么条件?

曲边四边形的面积, 没有公式可求，但若知道 8 个小曲边四边形的总面
积, 则只要用 8 个曲边四边形总面积除以 8，就可以得到每个小曲边四边形的面
积了,

(2) 要求 8 个小曲边四边形的总面积，根据题意需要什么条件?

8 个小曲边四边形恰好是圆环面积两两相交重亚一次的部分，因此只要
把五个圆环的总面积减去五个圆环盖住的总面积就可以了。

(3) 要求五个圆环的总面积，根据题意需要什么条件?

求出一个圆环的面积，然后乘以 5，就是五个圆环的总面积。

(4) 要求每个圆环的面积，需要什么条件?

已知圆环的内径 (4) 和外径 (5) ，然后按圆环面积公式求就是了。

圆环面积公式为:

S圆环=r (R2-r2)

= (Rrn (R-D

其思路可用下图 (图 2.5) 表示:

于
E
[请 了攻癌

外径避) 内径)
图2.5 ，