2022-2023学年人教版八年级数学上册第14章单元达标测试题及答案(Word版)

文档可直接打印使用,更多完整内容请关注官方网址https://jiandanjie.com 查询 或关注 #小程序:说明书指南

#公众号: 说明书指南

以下仅提取部分文档的文字供展示

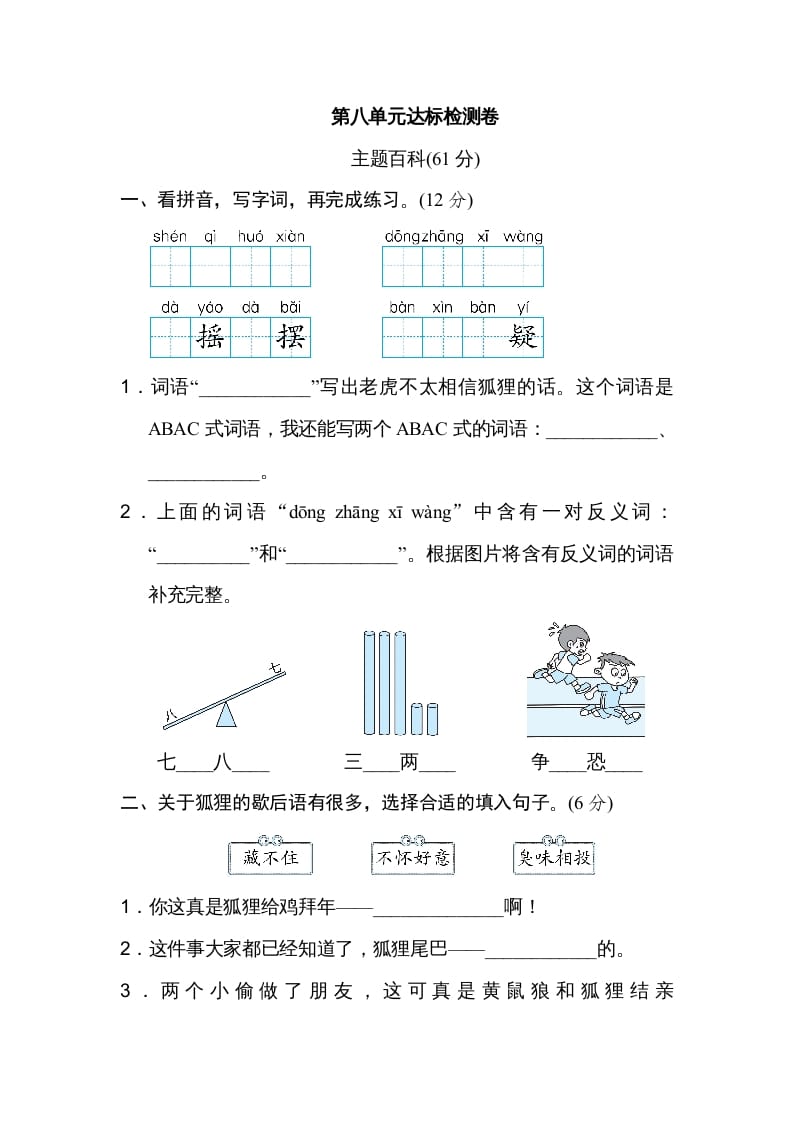
2022-2023 学年人教版八年级数学上册第 14 章单元达标测试题及答案

一. 选择题(共 10 小题，满分30 分)
下列运算正 确的是 5 )

2. 有 和式计算的是〔 )

有(2arD) (2方- 可 B. (2xrl) 5- 2x-1)
CC3r- 由(3xtbD D. (= mm 《四-四
3 把多项式 2冯 – 4x分解因式，应提取的公因式是〔 )
有 B. 2 8,，汪 D.

已知呈+ (CE 1) 0 个完全平方式，则大的值是【 )

A. 5 5或-3 所 :3 D.

5 下列各式从左到右， 人是 )
AD CH = -1
Br一区(CH -工
CCx-2) Cr-3) = (3-昌02-加
D. 六-dxt4一(2)
6. 长方形的面积为4了 – 8abt4a，若它的一边长为4a，则它的周长为《

4a -30 B， 10a – 4042 C，5a- 2b1 D.

3 证ya
7. 计算(-1=) X (<) ) 8 2 3 1 B. -1 CC “全 D 8 如果层- 2m- 4一0，那么代数式 (ar3) (m- 3) + (m- 2) “的值为《 6 1 D， 枉 ，则 a，久“的大小关系是【 ) 4 a>b>e Ba>c>b Ca51) 化简多项式4 时，小明的结果与其
贸他的几项中出现错误的是 正确的解答过程
《2) 小亮说:“只要给出 闻 – 2x+l 的合理的值，即可求出多项式 4 的值.”若给出达 – 2s+l 的值为 4，
请你求出此时 4的值.

同学的不同，请你检查以下小明同学的解题过程，在标

小明的作业
解:4= (rz+2)2+x(01-z) -9
= t+2rt4+tt一-9

外 @B
=3r-5

21.【观察发现】

从边长为 a的正方形中前掉一个边长为 5的正方形(如图@),然后将剩余部分剪开并拼成一个长方形(如
图四).

御 a 一>|
| 5

[5

图0 图@
【归纳结
《1) 上述操作，能验证的等式是 ，(直接写结果)

【问题解决】
《2) 利用〈1) 中的结论，计算:

上 1 1
区]人

1 1
人

22，阅读下列文字: 我们知道，对于 ，通过两种不同的方法计算它的面积，可忆
式. 图1给出了若干个边长为 和边长为&的小正方形纸片及若干个边长为 a、 六的长方

下列问，
51) 图2 是由图 1 提供的几何图形拼接而得，可以得到〔at太(at22)

52) 利用图 1 所给的纸片拼出一个长方形图形的面积为(2arb) (atb， 解决 问题: 若 4a+6abr2必
一60，atb=5，求 2at2的值。
53) 用图1 中关张边长为a的正方形, z张边长为上的正方形，z张边长分别为 a, 五的长方形纸片拼出

一个面积为《4at70) (6at50) 长方形，求 trz的值.
昌 昌

简单街-jiandanjie.com-学科网简单学习一条街 https://jiandanjie.com

23. 把代数式通过配凑等手段 得到局部完全平方式, 再进行有关运算和解题, 这种解题方法叫做配方法. 如:
人 可16at8

一dr6at8+t1 – 1一ai6at9 – 1一《at3)“
作光 – 2a – 1，利用配方法求必的最小值
解, – 2a- 1=好-2atl -2一 (a- 1
请根据上述材料解决下列问题:

《1) 用配方法因式分解: X+2x- 3.

(2) 若 司闻- 4xtl，求如的最小值
(3) 若 夺忆- 2a- 8b+17一0，求 at的值，

[ Cat3) +1H[ (at3) -了= (at4) (at2).。

(Ca- 1) ‘尖0..当a一1 时，如有最小值 – 2.

简单街-jiandanjie.com-学科网简单学习一条街 https://jiandanjie.com