七年级下册数学第六章第三节试卷及答案人教版(Word版)

文档可直接打印使用,更多完整内容请关注官方网址https://jiandanjie.com 查询 或关注 #小程序:说明书指南

#公众号: 说明书指南

以下仅提取部分文档的文字供展示

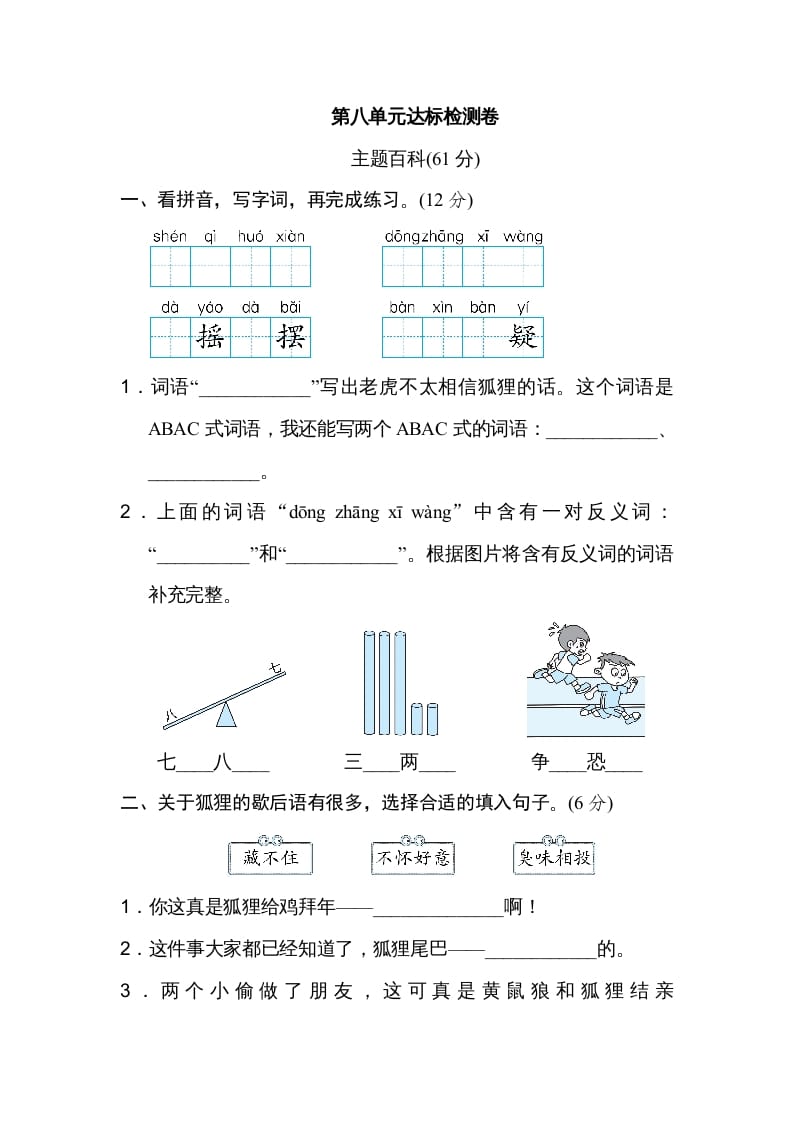
七年级下册数学第六章第三节试卷及答案人教版

一、 选择是
1 在-2，姓,上,314，沪也，三,这6个数中，无理数共有( 。 )

有A.工个 B. 2个 区机 D. 4个
2，有下列说法，其中正确说法的个数是( )

《1) 无理数就是开方开不尽的数，

52) 无理数是无限不循环小
53) 无理数包括正无理数、零、负无理数:
54) 无理数是无限不循环小数.

10 BILL CC 03

3. 荐Wa2- – a，则实数a 在数轴上的对应点一定在( )

A，原点左侧
C.，原点或

4 有理数只是有限小数。B。无理数是无限小数

5 无限小数是无理数 0， – 全是分数

5下列各组数中，瑟为相反数的组是《

人-25 (22 B -2和88 C -J52 D 1-2|和2
和(=-2) 和1=8 到

6. 如图，数轴上的点&、B、C、D 分别表示数 – 1、1、2、3，则表示2 – V5的点应在( )
A. 线段AI 上 B. 线段0上 5. 线段BC 上。 D. 线段CD 上

-、填空题
出一个大于3 且小于4 的无理数: 。 –

8，AW5的相反数是 ，倒数是 -es –
9.，写出两个无理数，使它们的和为有理炒 # 写出两个无理数，使它们的积为有理
数 《不能是一样的两数?

10. 在-13，n，0 好，2，一22，2.，121121112-.-(两个2之间依次多一个1)，0.3中。

51) 是有理数的有 一学
52) 是无理数的有 。
53) 是整数的有 。
54) 是分数的有

11.数轴上表示 1，AA2 的点为人,B, 且C.B两点到点上 的距离相等,则点C 所表示的数 –

简单街-jiandanjie.com-学科网简单学习一条街 https://jiandanjie.com

12. 根据图所示的拼图的启示填空.
1

|

面积为2

(计算VZ+AR = 和
他计算+AA2 =
后)计算V32 + ML28 = .

13.。 把下列各数填在相应的表示集合的大括号内:

1
一-3引，芋，-0. 3， 1. 7， ,0 ，1.， 1010010001… 《每两个1

2
多
之间依次多一个0)

整数{

负分数{

无理数{

14。(1) 求出下列各数，GD2 的平方根，@@-27 的立方根， 图VI6 的算术平方根.
62) 将〈1) 中求出的每个数准确地表示在数册上。

-0 1

53) 将〈1) 中求出的每个数按从小到大的顺序排列，并用“< ”连接. 简单街-jiandanjie.com-学科网简单学习一条街 https://jiandanjie.com
15. (本厦6 分) 在所给数轴上表示数-1，“WV7 ，“ |-对， 3 的相反数，并把这组数从
小到大用“<” 连接起来。 16. 试验与探究: 我们适分数写为小才 0.3，反之, 无限循环小数0 3成分炸 3 般地, 任何一个无限循环小数都可以写成分数形式. 现在就以07 为例进行讨论 设0 7 = 式， 池 由0 =0.7777…，可知，10x-x=7，77…-0，777…=7，即 10x-x=7，解方程得 。 9 ，于 是得 提 请仿照上述例题完成下列各古:〈本题4分) 《1) 请你把无限循环小数0.5 写成分数，即0.5= 《2 你能化无限循环小数0.73 为分数吗? 请仿照上 1 B 【解析】 试题分析， 无理数是指无限不循环小数， 本大中的无理数为了 和于。 人 【解析】 简单街-jiandanjie.com-学科网简单学习一条街 https://jiandanjie.com